Week 0 Friday#

Welcome to Math 10!

Canvas homepage

This class is an introduction to using Python for data science. There are two primary parts of the course:

  • Part 1. Exploratory Data Analysis. (Weeks 1-5)

  • Part 2. Introduction to Machine Learning. (Weeks 5-10)

Two in-class midterms: Monday Week 5 (10/30) and Monday Week 10 (12/04). They’re closed book and closed computer.

There’s no final exam; instead there is a class project.

There will be NO official textbook for this course. You may find the following references helpful:#

Announcements#

  • If you’re on the waitlist, please submit homework/take quizzes on the same schedule as the regular class. (Assignments won’t be excused, but I do drop the one lowest worksheet scores.)

What is Data Science?#

Three correlated concepts:

  • Data Science

  • Artificial Intelligence

  • Machine Learning

Battle of the Data Science Venn Diagrams

The original Venn diagram from Drew Conway:

Another diagram from Steven Geringer:

Perhaps the reality should be:

David Robinson’s Auto-pilot example:

  • Machine learning: predict whether there is a stop sign in the camera

  • Artificial intelligence: decide when to take the action of applying brakes (either by rules or from data)

  • Data science: provide the insights why it’s more likely to miss a stop sign before sunrise or after sunset

Example: Precision Medicine and Single-cell Sequencing.#

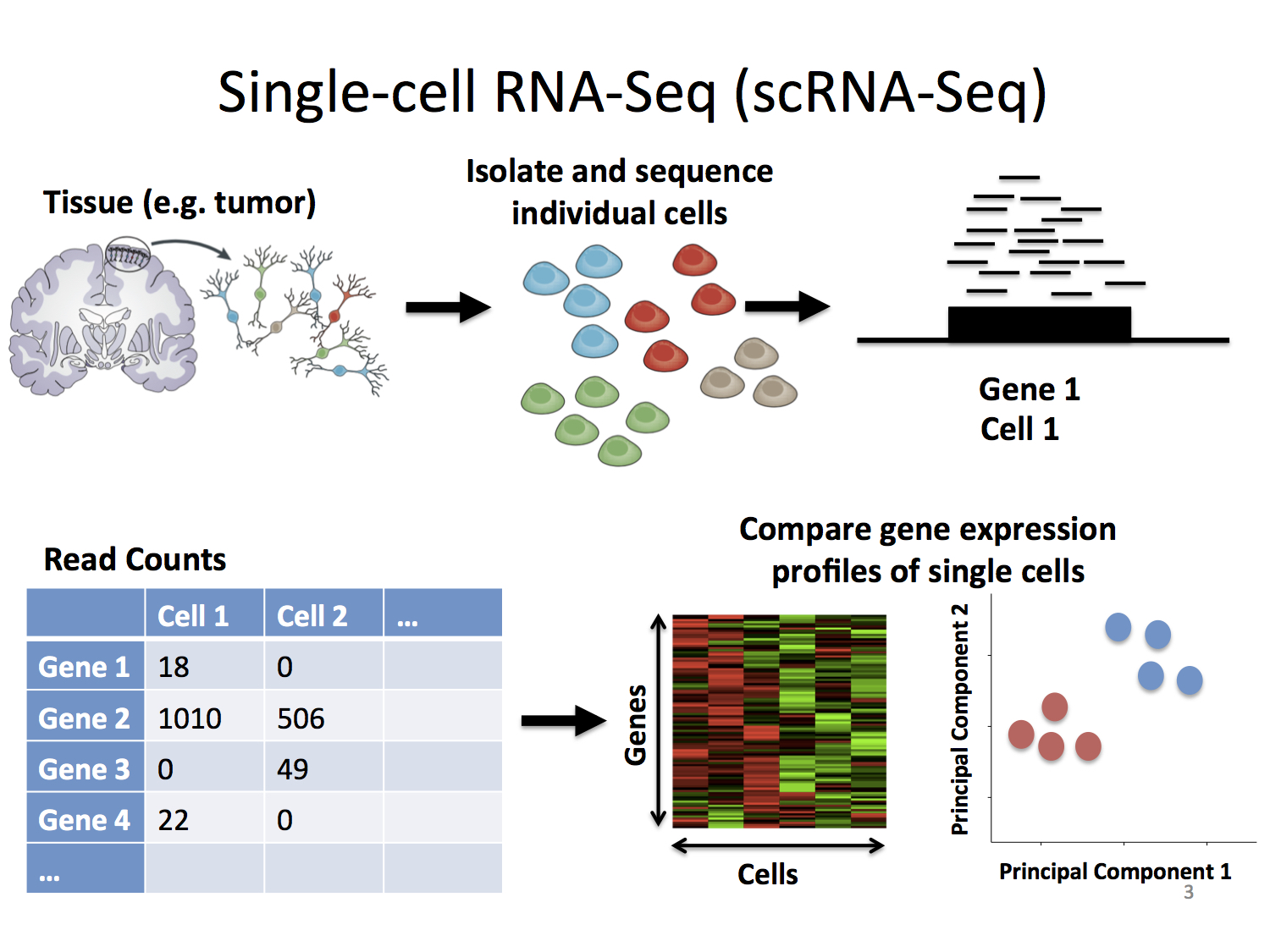
  • A structured data table, with \(n\) observations and \(p\) variables.

  • Mathematical representation: The data matrix \(X\in\mathbb{R}^{p\times n}\). For notations we write \(X=\left(\mathbf{x}^{(1)},\mathbf{x}^{(2)} \cdots, \mathbf{x}^{(n)} \right)\), where the \(i\)-th column vector represents \(i\)-th observation, \(\mathbf{x}^{(i)}=\left( \begin{matrix} x_{1}^{(i)}\\ x_{2}^{(i)} \\ \cdots \\ x_{p}^{(i)} \end{matrix} \right) \in\mathbb{R}^{p}\)

  • Roughly speaking, big data – large \(n\), high-dimensional data – large \(p\).

Why Python?#

Python is Good#

  • Stable Learning Curves

An entertaning cartoon from Tobias Hermann

  • Scalability of Computation (with the help with other packages)

benchmarking of scientific computation problems

comparison between Numpy and Matlab

Warm-up with Deepnote and some Python concepts#

You can type alone with me.

You execute a cell/block in Deepnote (or in a Jupyter notebook) by holding down shift and hitting return. The order in which you execute cells is important.

This is an example of a markdown cell. Markdown cells are used to write explanation for your code and format text nicely.

  • This is an example of making a list. To execute a cell, you can use command+enter. To edit a cell, make sure it’s highlighted, and then press enter.

Math 10#

Week 0#

Friday#

If you are fimilar with \(\LaTeX\)

  • \(\int_0^1 x^2 dx\)

Here’s an example of how we can change text color:

Warning: Midterm1 is on Week 5 Monday.

Here are some examples of code cells:

2+2

4

a = 4
b = 8
a+b

12

The order in which we evaluate cells matters!

print(x)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In [3], line 1
----> 1 print(x)

NameError: name 'x' is not defined

x = 10

print(x)

10

# take square of x
x**2

100

print('Hello World!')

Hello World!

list = [5, 6, 7, 8]

list[1]

6

Indexing in Python starts at 0!

list[0]

5

list[3]

8

list[-1]

8

list[::-1]

[8, 7, 6, 5]

  • NumPy is one of the most important python libraries

  • NumPy does not come with base python, we will need to import it every time we start a new notebook The abbreviation np is a standard convention, and we will always use it in Math 10.

# load Numpy
import numpy as np

# generate a random variable
# we can use the funtion in numpy random.default_rng

np.random.default_rng?

Docstring:
Construct a new Generator with the default BitGenerator (PCG64).

Parameters
----------
seed : {None, int, array_like[ints], SeedSequence, BitGenerator, Generator}, optional
    A seed to initialize the `BitGenerator`. If None, then fresh,
    unpredictable entropy will be pulled from the OS. If an ``int`` or
    ``array_like[ints]`` is passed, then it will be passed to
    `SeedSequence` to derive the initial `BitGenerator` state. One may also
    pass in a `SeedSequence` instance.
    Additionally, when passed a `BitGenerator`, it will be wrapped by
    `Generator`. If passed a `Generator`, it will be returned unaltered.

Returns
-------
Generator
    The initialized generator object.

Notes
-----
If ``seed`` is not a `BitGenerator` or a `Generator`, a new `BitGenerator`
is instantiated. This function does not manage a default global instance.

Examples
--------
``default_rng`` is the recommended constructor for the random number class
``Generator``. Here are several ways we can construct a random 
number generator using ``default_rng`` and the ``Generator`` class. 

Here we use ``default_rng`` to generate a random float:

>>> import numpy as np
>>> rng = np.random.default_rng(12345)
>>> print(rng)
Generator(PCG64)
>>> rfloat = rng.random()
>>> rfloat
0.22733602246716966
>>> type(rfloat)
<class 'float'>
 
Here we use ``default_rng`` to generate 3 random integers between 0 
(inclusive) and 10 (exclusive):
    
>>> import numpy as np
>>> rng = np.random.default_rng(12345)
>>> rints = rng.integers(low=0, high=10, size=3)
>>> rints
array([6, 2, 7])
>>> type(rints[0])
<class 'numpy.int64'>

Here we specify a seed so that we have reproducible results:

>>> import numpy as np
>>> rng = np.random.default_rng(seed=42)
>>> print(rng)
Generator(PCG64)
>>> arr1 = rng.random((3, 3))
>>> arr1
array([[0.77395605, 0.43887844, 0.85859792],
       [0.69736803, 0.09417735, 0.97562235],
       [0.7611397 , 0.78606431, 0.12811363]])

If we exit and restart our Python interpreter, we'll see that we
generate the same random numbers again:

>>> import numpy as np
>>> rng = np.random.default_rng(seed=42)
>>> arr2 = rng.random((3, 3))
>>> arr2
array([[0.77395605, 0.43887844, 0.85859792],
       [0.69736803, 0.09417735, 0.97562235],
       [0.7611397 , 0.78606431, 0.12811363]])
Type:      builtin_function_or_method

rng = np.random.default_rng()
rng.random(5)

array([0.78238483, 0.81217947, 0.52612065, 0.91363018, 0.65672153])

help(rng.random)

Help on built-in function random:

random(...) method of numpy.random._generator.Generator instance
    random(size=None, dtype=np.float64, out=None)
    
    Return random floats in the half-open interval [0.0, 1.0).
    
    Results are from the "continuous uniform" distribution over the
    stated interval.  To sample :math:`Unif[a, b), b > a` multiply
    the output of `random` by `(b-a)` and add `a`::
    
      (b - a) * random() + a
    
    Parameters
    ----------
    size : int or tuple of ints, optional
        Output shape.  If the given shape is, e.g., ``(m, n, k)``, then
        ``m * n * k`` samples are drawn.  Default is None, in which case a
        single value is returned.
    dtype : dtype, optional
        Desired dtype of the result, only `float64` and `float32` are supported.
        Byteorder must be native. The default value is np.float64.
    out : ndarray, optional
        Alternative output array in which to place the result. If size is not None,
        it must have the same shape as the provided size and must match the type of
        the output values.
    
    Returns
    -------
    out : float or ndarray of floats
        Array of random floats of shape `size` (unless ``size=None``, in which
        case a single float is returned).
    
    Examples
    --------
    >>> rng = np.random.default_rng()
    >>> rng.random()
    0.47108547995356098 # random
    >>> type(rng.random())
    <class 'float'>
    >>> rng.random((5,))
    array([ 0.30220482,  0.86820401,  0.1654503 ,  0.11659149,  0.54323428]) # random
    
    Three-by-two array of random numbers from [-5, 0):
    
    >>> 5 * rng.random((3, 2)) - 5
    array([[-3.99149989, -0.52338984], # random
           [-2.99091858, -0.79479508],
           [-1.23204345, -1.75224494]])

rng.random(3)

array([0.39916726, 0.40975624, 0.24989856])