Analysis of Electric Car Data

Analysis of Electric Car Data#

Author: Yongjun Zhu

Course Project, UC Irvine, Math 10, F23

Introduction#

Introduce your project here. Maybe 3 sentences.

In the era of sustainable transportation, electric vehicles (EVs) have emerged as a pivotal force reshaping the automotive landscape. As we witness a surge in the adoption of electric cars, understanding the nuances of their performance and efficiency becomes crucial for both consumers and industry stakeholders. This project delves into an analysis of electric car data, focusing on whether a diference in power train affect the range, top speed, efficiency.

Importing and Cleaning the data#

You can either have all one section or divide into multiple sections. To make new sections, use ## in a markdown cell. Double-click this cell for an example of using ##

import pandas as pd
import altair as alt
import seaborn as sns
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier

df = pd.read_csv("ElectricCarData_Clean.csv")
df

	Brand	Model	AccelSec	TopSpeed_KmH	Range_Km	Efficiency_WhKm	FastCharge_KmH	RapidCharge	PowerTrain	PlugType	BodyStyle	Segment	Seats	PriceEuro
0	Tesla	Model 3 Long Range Dual Motor	4.6	233	450	161	940	Yes	AWD	Type 2 CCS	Sedan	D	5	55480
1	Volkswagen	ID.3 Pure	10.0	160	270	167	250	Yes	RWD	Type 2 CCS	Hatchback	C	5	30000
2	Polestar	2	4.7	210	400	181	620	Yes	AWD	Type 2 CCS	Liftback	D	5	56440
3	BMW	iX3	6.8	180	360	206	560	Yes	RWD	Type 2 CCS	SUV	D	5	68040
4	Honda	e	9.5	145	170	168	190	Yes	RWD	Type 2 CCS	Hatchback	B	4	32997
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
98	Nissan	Ariya 63kWh	7.5	160	330	191	440	Yes	FWD	Type 2 CCS	Hatchback	C	5	45000
99	Audi	e-tron S Sportback 55 quattro	4.5	210	335	258	540	Yes	AWD	Type 2 CCS	SUV	E	5	96050
100	Nissan	Ariya e-4ORCE 63kWh	5.9	200	325	194	440	Yes	AWD	Type 2 CCS	Hatchback	C	5	50000
101	Nissan	Ariya e-4ORCE 87kWh Performance	5.1	200	375	232	450	Yes	AWD	Type 2 CCS	Hatchback	C	5	65000
102	Byton	M-Byte 95 kWh 2WD	7.5	190	400	238	480	Yes	AWD	Type 2 CCS	SUV	E	5	62000

103 rows × 14 columns

df.isnull().values.any()

False

Since the output is false, this Dataset is clean. After make sure that the data is clean, we now need to basicly describe the relevant variables I would use.

# Calculate mean, median, standard deviation
mean_Efficiency_WhKm = df['Efficiency_WhKm'].mean()
median_Efficiency_WhKm = df['Efficiency_WhKm'].median()
std_Efficiency_WhKm = df['Efficiency_WhKm'].std()
print (mean_Efficiency_WhKm)
print (median_Efficiency_WhKm)
print (std_Efficiency_WhKm)

16504854368932
0
566839230892835

mean_TopSpeed_KmH = df['TopSpeed_KmH'].mean()
median_TopSpeed_KmH = df['TopSpeed_KmH'].median()
std_TopSpeed_KmH = df['TopSpeed_KmH'].std()
print (mean_TopSpeed_KmH)
print (median_TopSpeed_KmH)
print (std_TopSpeed_KmH)

19417475728156
0
573030481499785

mean_Range_Km = df['Range_Km'].mean()
median_Range_Km = df['Range_Km'].median()
std_Range_Km = df['Range_Km'].std()
print (mean_Range_Km)
print (median_Efficiency_WhKm)
print (std_Efficiency_WhKm)

7864077669903
0
566839230892835

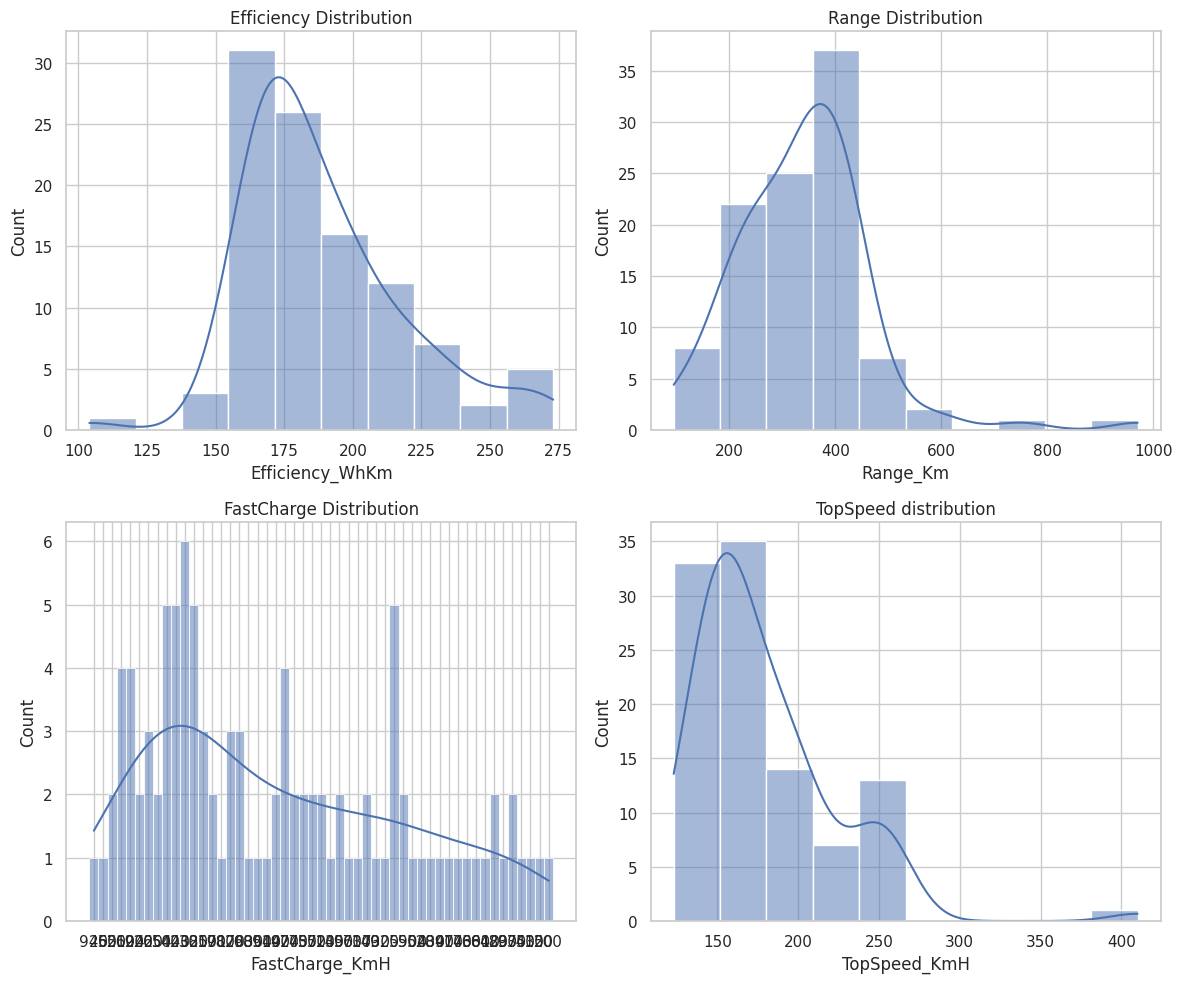
For efficiency, the mean and median are close, indicating a symmetric distribution. The relatively low standard deviation suggests consistency in acceleration values. For top speed, the mean is higher than the median, suggesting a right-skewed distribution with a few vehicles having very high top speeds. For range, the mean is significantly higher than the median, indicating a right-skewed distribution with a few vehicles having much longer ranges.

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import geopandas as gpd
from mpl_toolkits.axes_grid1 import make_axes_locatable
sns.set(style="whitegrid")
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(12, 10))
sns.histplot(df['Efficiency_WhKm'], bins=10, kde=True, ax=axes[0, 0])
axes[0, 0].set_title('Efficiency Distribution')
sns.histplot(df['Range_Km'], bins=10, kde=True, ax=axes[0, 1])
axes[0, 1].set_title('Range Distribution')
sns.histplot(df['FastCharge_KmH'], bins=10, kde=True, ax=axes[1, 0])
axes[1, 0].set_title('FastCharge Distribution')
sns.histplot(df['TopSpeed_KmH'], bins=10, kde=True, ax=axes[1, 1])
axes[1, 1].set_title('TopSpeed distribution')
plt.tight_layout()
plt.show()

../../_images/06d72d6869538ab7a151bf51ac371ad33669c48d8c2d0c0694a14fd728a1f128.png

Predicting Factor Whether Diffference in Power Train is Important.#

I want to explore whether a diference in power train affect the range, top speed, or efficiency. For example, does AWD has a higher top speed than RWD or does RWD has a higher efficiency?

Decision Tree Regression#

df

	Brand	Model	AccelSec	TopSpeed_KmH	Range_Km	Efficiency_WhKm	FastCharge_KmH	RapidCharge	PowerTrain	PlugType	BodyStyle	Segment	Seats	PriceEuro
0	Tesla	Model 3 Long Range Dual Motor	4.6	233	450	161	940	Yes	AWD	Type 2 CCS	Sedan	D	5	55480
1	Volkswagen	ID.3 Pure	10.0	160	270	167	250	Yes	RWD	Type 2 CCS	Hatchback	C	5	30000
2	Polestar	2	4.7	210	400	181	620	Yes	AWD	Type 2 CCS	Liftback	D	5	56440
3	BMW	iX3	6.8	180	360	206	560	Yes	RWD	Type 2 CCS	SUV	D	5	68040
4	Honda	e	9.5	145	170	168	190	Yes	RWD	Type 2 CCS	Hatchback	B	4	32997
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
98	Nissan	Ariya 63kWh	7.5	160	330	191	440	Yes	FWD	Type 2 CCS	Hatchback	C	5	45000
99	Audi	e-tron S Sportback 55 quattro	4.5	210	335	258	540	Yes	AWD	Type 2 CCS	SUV	E	5	96050
100	Nissan	Ariya e-4ORCE 63kWh	5.9	200	325	194	440	Yes	AWD	Type 2 CCS	Hatchback	C	5	50000
101	Nissan	Ariya e-4ORCE 87kWh Performance	5.1	200	375	232	450	Yes	AWD	Type 2 CCS	Hatchback	C	5	65000
102	Byton	M-Byte 95 kWh 2WD	7.5	190	400	238	480	Yes	AWD	Type 2 CCS	SUV	E	5	62000

103 rows × 14 columns

cols = ["TopSpeed_KmH", "Range_Km",'Efficiency_WhKm']
clf = DecisionTreeClassifier(max_leaf_nodes=3, random_state=2)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(df[cols], df["PowerTrain"], test_size=0.1, random_state=1)

clf.fit(X_train, y_train)

DecisionTreeClassifier(max_leaf_nodes=3, random_state=2)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

fig = plt.figure()
_ = plot_tree(clf, 
                   feature_names=clf.feature_names_in_,
                   class_names=clf.classes_,
                   filled=True)

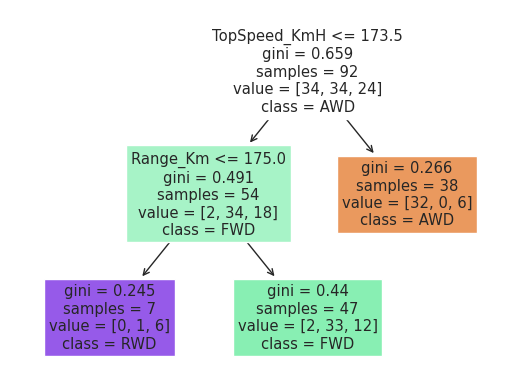
../../_images/33af7e4a9144c437723cc63332e2e61ad3753788dd10a7d0d3f594b6486846ba.png

clf.score(X_test, y_test)

0.9090909090909091

clf.classes_

array(['AWD', 'FWD', 'RWD'], dtype=object)

rng = np.random.default_rng()
arr = rng.random(size = (5000,3))
df2 = pd.DataFrame(arr, columns=cols)
df2.head(100)
df2["TopSpeed_KmH"] *= 533
df2["Range_Km"] *= 2000
df2['Efficiency_WhKm']*= 1500
df2['pred'] = clf.predict(df2[cols])
df2

	TopSpeed_KmH	Range_Km	Efficiency_WhKm	pred
0	75.763884	255.966114	900.393787	FWD
1	216.167973	987.532089	507.045214	AWD
2	230.895722	911.609365	734.088010	AWD
3	168.836826	410.808157	122.222156	FWD
4	118.586470	280.029296	1214.505492	FWD
...	...	...	...	...
4995	400.444607	1747.976327	1220.161437	AWD
4996	365.754845	1779.344836	742.714966	AWD
4997	362.125188	593.176167	5.623374	AWD
4998	222.911450	1436.147150	395.546491	AWD
4999	234.150228	875.772255	273.838896	AWD

5000 rows × 4 columns

alt.Chart(df2).mark_circle().encode(
    x = "TopSpeed_KmH",
    y = "Efficiency_WhKm",
    color = 'pred'
)

Thus, from the above graph, we can easily see that the power train is irrelevant to efficiency of those EVs. However, the topspeed does. Even if the top speeds of FWD and RWD are almost the same, both smaller than 173.5km/h, cars with AWD can drive much faster than RWD and FWD.

alt.Chart(df2).mark_circle().encode(
    x = "TopSpeed_KmH",
    y = "Range_Km",
    color = 'pred'
)

From the above graph, we can see that compare to RWD, FWD EVs has more range. While, still, AWD get the highest topspeed. It seems that power train related to the range and the topspeed, instead of the efficiency.

alt.Chart(df2).mark_circle().encode(
    x = "Efficiency_WhKm",
    y = "Range_Km",
    color = 'pred'
)

This graph proves our thoughts above that the data of eficiency are all random, and only RWD and FWD affect the range.

Some Concerns about the Relation#

We do show that the power training does affected EVs’ topspeed and range. However, price is also a primary effect. In our common sense, FWD and RWD vehicles are more affordable, while AWD EVs are more expensive. Let’s us check whether price is also affected.

df

	Brand	Model	AccelSec	TopSpeed_KmH	Range_Km	Efficiency_WhKm	FastCharge_KmH	RapidCharge	PowerTrain	PlugType	BodyStyle	Segment	Seats	PriceEuro
0	Tesla	Model 3 Long Range Dual Motor	4.6	233	450	161	940	Yes	AWD	Type 2 CCS	Sedan	D	5	55480
1	Volkswagen	ID.3 Pure	10.0	160	270	167	250	Yes	RWD	Type 2 CCS	Hatchback	C	5	30000
2	Polestar	2	4.7	210	400	181	620	Yes	AWD	Type 2 CCS	Liftback	D	5	56440
3	BMW	iX3	6.8	180	360	206	560	Yes	RWD	Type 2 CCS	SUV	D	5	68040
4	Honda	e	9.5	145	170	168	190	Yes	RWD	Type 2 CCS	Hatchback	B	4	32997
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
98	Nissan	Ariya 63kWh	7.5	160	330	191	440	Yes	FWD	Type 2 CCS	Hatchback	C	5	45000
99	Audi	e-tron S Sportback 55 quattro	4.5	210	335	258	540	Yes	AWD	Type 2 CCS	SUV	E	5	96050
100	Nissan	Ariya e-4ORCE 63kWh	5.9	200	325	194	440	Yes	AWD	Type 2 CCS	Hatchback	C	5	50000
101	Nissan	Ariya e-4ORCE 87kWh Performance	5.1	200	375	232	450	Yes	AWD	Type 2 CCS	Hatchback	C	5	65000
102	Byton	M-Byte 95 kWh 2WD	7.5	190	400	238	480	Yes	AWD	Type 2 CCS	SUV	E	5	62000

103 rows × 14 columns

cols2 = ["TopSpeed_KmH", "Range_Km",'PriceEuro']
clf = DecisionTreeClassifier(max_leaf_nodes=3, random_state=2)
from sklearn.model_selection import train_test_split
X_train_copy, X_test_copy, y_train_copy, y_test_copy = train_test_split(df[cols2], df["PowerTrain"], test_size=0.1, random_state=1)

clf.fit(X_train_copy, y_train_copy)

DecisionTreeClassifier(max_leaf_nodes=3, random_state=2)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

clf.score(X_test_copy, y_test_copy)

0.7272727272727273

rng = np.random.default_rng()
arr = rng.random(size = (5000,3))
df3 = pd.DataFrame(arr, columns=cols2)
df3.head(100)
df3["TopSpeed_KmH"] *= 533
df3["Range_Km"] *= 2000
df3['PriceEuro']*= 150000
df3['pred'] = clf.predict(df3[cols2])
df3

	TopSpeed_KmH	Range_Km	PriceEuro	pred
0	477.074797	236.322462	105212.397918	AWD
1	264.183237	148.540958	17435.334464	RWD
2	501.443481	1650.618871	120598.841358	AWD
3	85.999767	1937.402358	28153.593600	FWD
4	235.734838	645.247924	120656.262036	AWD
...	...	...	...	...
4995	296.087939	1224.857933	51461.448756	AWD
4996	59.041436	664.649628	51193.516643	AWD
4997	52.304701	567.583976	141330.737613	AWD
4998	70.680920	1163.603349	70373.781378	AWD
4999	123.760752	1991.547730	131496.304429	AWD

5000 rows × 4 columns

alt.Chart(df3).mark_circle().encode(
    x = "TopSpeed_KmH",
    y = "PriceEuro",
    color = 'pred'
)

Thus, we found that AWD EVs have higher price than FWD and RWD. Due to this high price, it is reasonable for AWD to have a higher topspeed but not range.

Summary#

Normally, all else being equal, AWD vehicles tend to have slightly lower ranges compared to their RWD or FWD counterparts. This is because AWD systems generally involve more components and increased weight, which can affect energy efficiency. However, since in reality, AWD EVs always have a hgher price, this “slightly low” might not reflect from the analysis. The choice of powertrain can influence the top speed capabilities of an electric vehicle. AWD vehicles might have higher top speeds, especially in performance-oriented models, due to improved traction and stability. Generally, FWD electric vehicles tend to be more energy-efficient compared to AWD models. This is because AWD systems introduce additional mechanical components and increase the overall weight of the vehicle.

References#

Your code above should include references. Here is some additional space for references.

What is the source of your dataset(s)?

Datasource: ev-database.org/
Banner image: freepik - author - ‘macrovector’

List any other references that you found helpful.

AWD, FWD, or RWD—Which Wheel Drive Is Best?

Front-Wheel Drive vs. Rear-Wheel Drive | Pros & Cons ()

Analysis of Electric Car Data

Contents

Analysis of Electric Car Data#

Introduction#

Importing and Cleaning the data#

Predicting Factor Whether Diffference in Power Train is Important.#

Decision Tree Regression#

Some Concerns about the Relation#

Summary#

References#